Explainable AI - Methods for explaining AI models

Post-hoc approaches for XAI

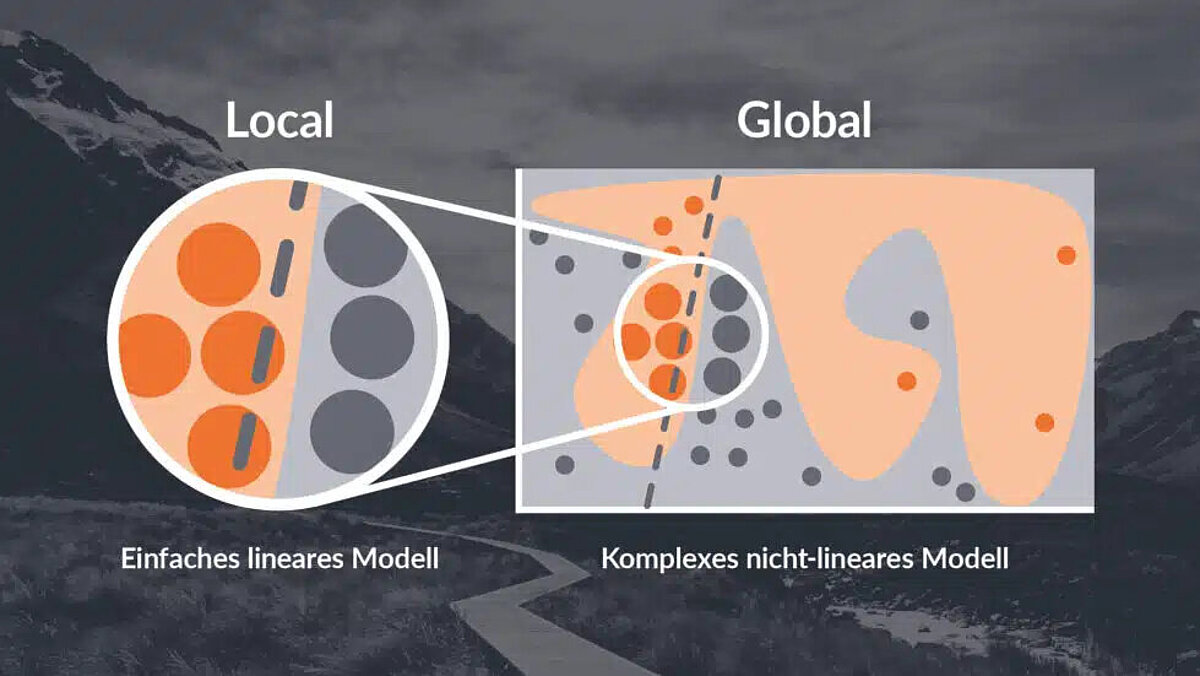
There is now a well-stocked toolbox of methods that enable the analysis and evaluation of the decision logic of a black-box model—i.e., a model whose decision logic is not transparent. In principle, however, many methods follow similar approaches. We therefore describe here a number of approaches that can be used to make a black box transparent or at least dark-tinted rather than jet black, depending on the approach and complexity. As a rule, post-hoc methods are divided into global and local approaches.

• Global methods attempt to map and interpret an entire model. The goal is to understand the general decision logic of the model. One example is to train an explainable model with all available inputs and outputs of a black box model and examine the new explainable model for its decision logic.
• Local methods examine a model's decision for a specific input to understand how that specific input leads to the corresponding output. Examples include methods that repeatedly make slight changes to a specific input and use these new variants to examine the behavior of the model.

In addition, the methods can be model-agnostic or model-specific. Here, we focus on model-agnostic methods that can be applied to any type of AI model. Model-specific methods are methods that can only be applied to a specific type of AI model. Below, we summarize some of the most common model-agnostic XAI methods for tabular data.

Global methods

Global Surrogate Models

In this approach, the behavior of a black-box model is analyzed using an explainable model. All that is needed for this is a dataset of inputs and outputs from the black box. This data set can then be used to train an explainable model, such as a linear regression. However, caution is advised, as the quality of this “explanation” depends heavily on the quality of the data set. In addition, the simpler explainable model may not be able to map the complex decision logic of the black-box model. Conversely, if a simplified surrogate model can be found that can completely replicate the output of the complex model, the complexity of the model under investigation can of course be questioned.

Permutation Feature Importance

The concept behind this method is relatively simple: if a feature is important for the decision of an AI model, the prediction quality of the model should deteriorate if this feature is made unrecognizable. To test this, the values of a feature are randomly shuffled across all examples in a dataset so that there is no longer any meaningful correlation between the new value of the feature and the target value for an example. If this significantly increases the error made by the AI model in its predictions, the feature is rated as important. If this is not the case, or only to a lesser extent, the feature is considered less important.

Causal Discovery

An interesting, but somewhat more complex method is causal discovery. Here, an undirected graph is created based on the correlation matrix of the data. This graph connects all features and result variables in a network – the graph. This network is then reduced to the necessary size and complexity using optimization methods. The result is a graph from which causalities can be derived. More specifically, the effect of the individual features on the result of the model can be intuitively deduced from the graph. However, even such methods come with no guarantees. Reliable and stable results for such explanatory models are difficult to obtain because the resulting graphs are often very sensitive to the selected input.

Local methods

Local Surrogate Models (LIME)

LIME (Local interpretable model-agnostic explanations) involves training a local “surrogate model” for an example. Put simply, LIME takes a defined input (an example), processes it through the black-box model, and then analyzes the output. The features of the example are then slightly altered one by one, and the new example is sent through the black-box model again. This process is repeated many times. This allows an explainable model to be created, at least around the initial example, which shows the influence of the features on the output. Using the example of automatic claim processing by a car insurance company, this would mean repeatedly changing the features of a claim slightly (vehicle type, age, gender, amount, etc.) and testing how the AI model's decision changes as a result.

SHAP

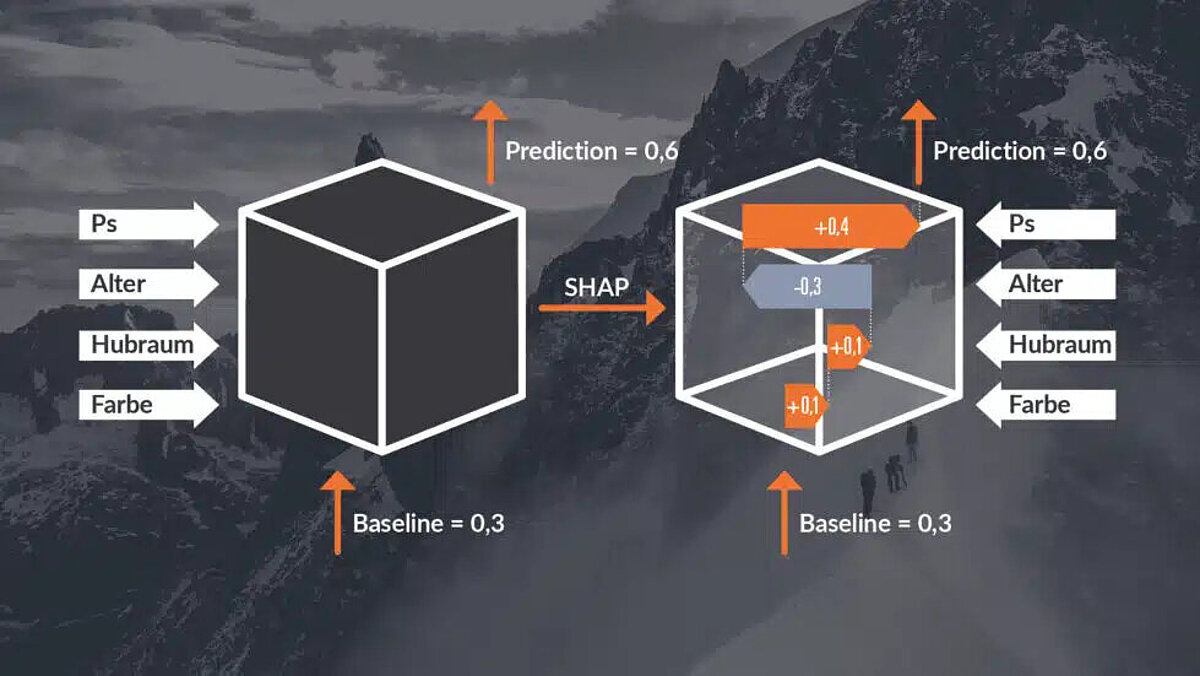
SHAP (SHapley Additive exPlanations) can be used to analyze how much influence certain features have on the model's prediction for a specific example. SHAP does this by analyzing the importance of certain features for the output using permutation of the input features. In this case, permutation means that the values for certain features are replaced with the values from other examples in the dataset. This idea is based on Shapley Values, which originate from game theory. The output of a model is understood as the winnings in a cooperative game, while the features represent the players. The permutations are used to determine how much each “player” (feature) contributes to the “win” (output). A major advantage of SHAP is that it can produce both local and global explanations. SHAP is one of the most popular XAI methods, although the very high number of permutations requires considerable computing power.

CXPlain

CXPlain is a newer method that attempts to retain the strengths of methods such as LIME or SHAP while avoiding their disadvantages, such as high computing times. Instead of training an explainable model that emulates the black-box AI model or testing numerous permutations, CXPlain trains a standalone model that estimates the importance of individual features. The model is trained based on the errors of the original black-box AI model, and can thus provide an estimate of which features make the greatest contribution to the prediction of the black-box AI model. In addition, CXPlain provides an estimate of how confident the model is in its predictions – and thus also of the uncertainty associated with the results. This is not the case with other XAI methods.

Counterfactuals

What would have to change in the input for the output to change? This is the question asked when using counterfactuals. Here, the minimum changes required to change the output of a model are determined. To make this possible, new synthetic examples are generated, and the best ones are selected. Take the example of credit scoring: How much would the age or assets of the applicant have to change for a loan to be granted instead of rejected? For example, would change the gender from “female” to “male” result in the loan being granted? This allows us to identify unwanted distortions or biases in the model's predictions. The situation is similar in the example of automatic claim processing for car insurance. We ask: “What characteristics of the policyholder would have to be changed at a minimum to change the model's decision?”

Why not build white-box models directly?

In general, all the methods described here refer to post-hoc interpretation of models. However, it should not be forgotten that many problems can already be solved with existing comprehensible models. Methods such as regressions or decision trees can solve many business use cases and are explainable. However, particularly complicated or larger problems require the use of more complex models. To make these explainable, we use the methods described here, among others, in practice. Producing explainable models is currently one of the core areas of application for AI. This is particularly emphasized by current legislation such as the European AI Act, which makes explainability a mandatory feature of AI models in critical areas. Of course, it also makes intuitive sense to prefer explainable models. Who would want to sit in a self-driving car controlled by AI that is so complex that not even the manufacturers know how and why the AI makes its decisions?