Methoden der Imputation und wann sie eingesetzt werden sollten

Warum uns fehlende Werte interessieren sollten

In unserer Arbeit als Data Scientists arbeiten wir häufig mit Zeitreihendaten und Anwendungen für Prognosen (=Forecasting). Wie bei allen „klassischen“ Projekten des maschinellen Lernens gibt es auch beim Forecasting oft fehlende Daten, mit denen wir umgehen müssen.

Für das Forecasting sind fehlende Werte besonders problematisch, weil die Modelle in der Regel zeitabhängige Merkmale (=Features) enthalten. Zeitabhängige Features sind in der Regel verzögerte oder saisonale Merkmale. Wenn die Muster dieser Features unterbrochen sind, haben die Modelle Schwierigkeiten, diese Muster zu lernen. Außerdem können die meisten klassischen Prognosemethoden wie ARIMA-Modelle nicht automatisch mit fehlenden Werten umgehen.

Der erste wichtige Schritt beim Umgang mit fehlenden Werten in Zeitreihen ist – wie so häufig – die Analyse der Daten. Diese Analyseschritte können dabei helfen, festzustellen, ob die Daten zufällig fehlen oder nicht. Wenn Werte nicht zufällig fehlen und vom spezifischen Prognosekontext abhängen, können in der Regel automatisierten Methoden nicht mit den Auswirkungen umgehen, und es ist Fachwissen erforderlich, um diese Fälle zu behandeln. 

Ein Beispiel für nicht zufällig fehlende Daten ist die Vorhersage von Ladenverkäufen, bei denen die Daten an Feiertagen immer fehlen. An diesen Tagen ist der Umsatz gleich Null, und an den Tagen vor und nach dem Feiertag steigt der Umsatz normalerweise an. Eine Methode zur Bewältigung dieses Problems könnte darin bestehen, Merkmale wie „Feiertag“ oder „Tag nach dem Feiertag“ in das Modell aufzunehmen.

Ein Beispiel für zufällig fehlende Daten könnten Unfälle oder Fehler sein, die bei der Übertragung von Daten aus dem operativen System in ein Data Warehouse aufgetreten sind. Diese Unfälle hingen nicht von den Daten ab und passierten zufällig zu einem bestimmten Zeitpunkt. Handelt es sich hingegen um einen Fehler, der regelmäßig zu bestimmten Tages- oder Wochenzeiten auftritt, so würde es sich wiederum um nicht zufällig fehlende Daten handeln.

Grundsätzlich ist es bei der Durchführung der Analyse wichtig, auf folgende Details zu achten:

• Wie hoch ist der Prozentsatz der fehlenden Daten im Verhältnis zum Gesamtumfang?
• Treten die Lücken in regelmäßigen Abständen auf?
• Wie groß ist die Länge der Lücken?

Die wichtigsten Methoden der Imputation und was bei ihrer Anwendung zu beachten ist

Die meisten der Methoden, die wir hier auflisten, sind bekannt und bereits in wissenschaftlichen Arbeiten und anderen Online-Quellen gut beschrieben. In diesem Artikel wollen wir vor allem die verschiedenen Methoden miteinander vergleichen und Hinweise geben, wann welche Methode zu verwenden ist.

Die erste und bei weitem einfachste Methode zum Umgang mit fehlenden Daten ist das Löschen dieser Daten. Diese Lösung kann bei einigen klassischen Problemen des maschinellen Lernens hilfreich sein, aber in der Regel nicht bei Zeitreihen. Wie bereits erwähnt, werden dadurch die Muster der Zeitreihen unterbrochen und das Modell lernt aus falschen Mustern. Dennoch ist es möglich, nur den „gesunden“ Teil des Datensatzes auszuwählen, wenn dies im Hinblick auf die angestrebten Ziele sinnvoll ist. So könnte eine praktikable Lösung darin bestehen, die erste Hälfte der Datenreihe zu verwerfen, wenn die Qualität von da an besser ist (z. B., weil sich der Datenerfassungsprozess zu einem bestimmten Zeitpunkt geändert hat). Diese Option kommt nur in Frage, wenn wir genügend Daten haben, um die Modelle zu trainieren.

Wenn das Löschen von Daten nicht in Frage kommt, müssen wir einige Imputationsmethoden anwenden, d. h. Methoden zum Auffüllen der fehlenden Werte. Eine Familie der Imputationsmethoden verwendet den Mittelwert. Hier besteht die Idee darin, die fehlenden Werte mit dem globalen, lokalen oder saisonalen Mittelwert aufzufüllen, um einen angemessenen Ersatzwert zu erhalten. Jede dieser Methoden ist in verschiedenen Zusammenhängen nützlich, je nach Trend und Saisonalität der Daten. Eine weitere Möglichkeit besteht darin, die fehlenden Werte mit dem vorherigen oder dem nächsten verfügbaren Wert aufzufüllen, was als forward bzw. backward fill bezeichnet wird.

Die letzte Familie der Imputationsmethoden, die wir hier erwähnen wollen, ist die Interpolation, d. h. das Einfügen fehlender Werte in den Beobachtungsbereich einer Zeitreihe. Diese Interpolation kann linear, polynomial oder spline sein, was die Art der Kurve definiert, die zur Modellierung der Daten verwendet wird. Eine lineare Interpolation kann auch an die Saisonalität angepasst werden (dies wird im Folgenden als linear angepasst bezeichnet). Eine weitere Interpolationsmethode ist die Verwendung von Holt-Winters, einer exponentiellen Glättung dritten Grades, die das Niveau (erster Grad), den Trend (zweiter Grad) und die Saisonalität (dritter Grad) der linearen Interpolation der Lücken erfasst.

Der nachstehende Entscheidungsbaum fasst unsere Entscheidungen zusammen und konsolidiert die von uns meist verwendete Faustregel. Auch wenn es sich um einen guten Anhaltspunkt handelt, müssen wir mit genaueren Metriken und dem Sehtest prüfen, d. h. wir stellen die unterstellten Werte verschiedener Methoden dar, um zu prüfen, welche am besten zum Muster der Zeitreihe passt, und den Modellen hilft, genauere Prognosen zu erstellen.

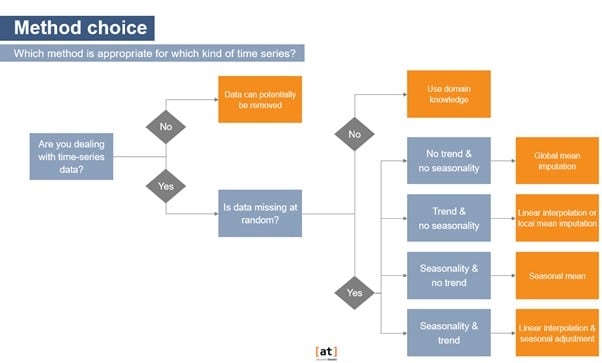
Die Bewertung der Qualität von Imputationsmethoden

Für ein besseres Verständnis der Schritte, die wir normalerweise bei der Imputation fehlender Werte befolgen, betrachten wir ein konkretes Beispiel. Hier beginnen wir mit einem vollständigen Datensatz und erzeugen darin künstlich fehlende Werte, um die imputierten Werte mit den echten zu vergleichen. Wir haben einen Datensatz aus der Store Item Demand Forecasting Challenge auf Kaggle verwendet, der Verkaufsdaten aus fünf Jahren für 50 verschiedene Artikel in 10 verschiedenen Geschäften enthält. Wie bereits erwähnt, ist der Datensatz sauber und enthält keine fehlenden Werte. Um die Komplexität zu reduzieren, haben wir die Daten auf eine monatliche Frequenz aggregiert.  

Wir haben eine Funktion entwickelt, die nach dem Zufallsprinzip einen vordefinierten Prozentsatz fehlender Werte in die Zeitreihe einfügt, mit der Option, die Lücken zu parametrisieren (Anzahl und maximale Länge). Mit dieser Funktion können wir verschiedene Prozentsätze fehlender Daten und Lückenlängen ausprobieren. In diesem Beispiel gibt es sechs Lücken, wobei die längste drei Monate lang ist und 10 % der Zeitreihe fehlen.

Da der Datensatz nun fehlende Werte enthält, wenden wir einige der oben aufgeführten Methoden an und stellen sie den realen Daten gegenüber, indem wir sie visualisieren und mit Metriken vergleichen. Im folgenden Beispiel haben wir dies nur auf eine der Zeitreihen aus dem Datensatz angewandt, während wir es in einem realen Projekt wahrscheinlich mit sehr viel mehr Zeitreihen zu tun hätten. 

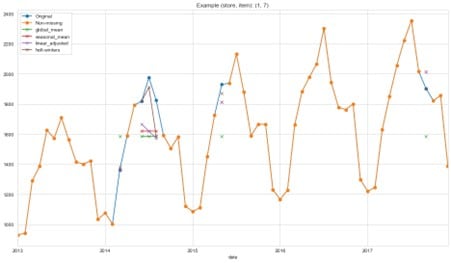
In der nachstehenden Grafik sieht man die Verkaufsdatensätze für Artikel 7 von Geschäft 1. Die orangefarbene Linie beschreibt die vollständigen Daten, die uns vorliegen. Die blaue Linie zeigt die Daten, die wir für unsere Experimente aus der Reihe entfernt haben. Die kleinen Kreuze in verschiedenen Farben zeigen die unterstellten Werte, die mit verschiedenen Methoden berechnet wurden. Man kann erkennen, dass die linear angepasste und die Holt-Winters-Imputationsmethode besser in der Lage sind, die Variationen unserer Zeitreihe zu erfassen. Weil die Daten einen Trend und Saisonalität enthalten, schneiden die beiden Methoden, die Trend und Saisonalität berücksichtigen, am besten ab.  Dies bestätigt die Faustregel, die wir in der obigen Abbildung dargestellt haben.

Da es unser Ziel ist, das beste Vorhersageergebnis für künftige Zeiträume zu erzielen, wollen wir die Auswirkungen der verschiedenen Imputationsmethoden auf ein Vorhersagemodell messen. Daher haben wir dasselbe Prognosemodell für jede Methode angepasst und die Fehler für den Testsatz (das letzte Jahr der Reihe) anhand der folgenden klassischen Regressionsbewertungs-Metriken verglichen: 

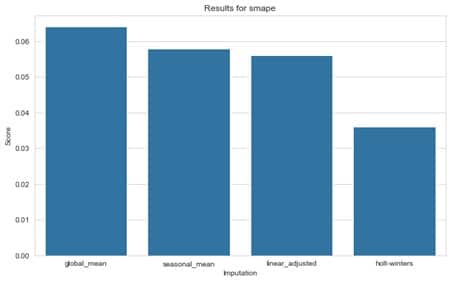
• Der symmetrische mittlere absolute Fehler in Prozent (sMAPE) oder die mittlere absolute Abweichung in Prozent, die die Genauigkeit als Verhältnis ausdrückt. Er ist sehr intuitiv, kann aber aufgrund einer kleinen Fehlerabweichung (bei einer Reihe von kleinen Nennern) sehr groß werden.
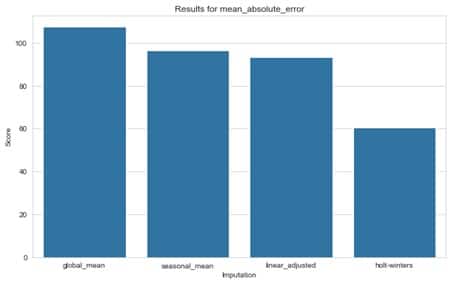
• Der mittlere absolute Fehler (MAE), der den Abstand zwischen den einzelnen Prognosen und dem tatsächlichen Wert misst, ist einfacher zu interpretieren.

Untenstehend finden sich die Ergebnisse des Prognosemodells für die verschiedenen Imputationsmethoden. Wie bereits im obigen Schaubild angedeutet, zeigt sich, dass die Holt-Winters-Methode und die linear angepasste Imputation bessere Vorhersageergebnisse liefern als die Mittelwertmethode. Es zeigt sich jedoch auch, dass die Ergebnisse der Methode des saisonalen Mittelwerts mit denen der linear bereinigten Methode vergleichbar sind. Dies bestätigt, dass man mehrere Methoden ausprobieren und vergleichen sollte, anstatt sich nur auf die Faustregel zu verlassen. Außerdem sehen wir, dass beide Metriken das gleiche Ergebnis anzeigen, was uns in unserer Schlussfolgerung bestärkt.

Natürlich war das nur ein Modell für eine Zeitreihe, und in einem realistischen Beispiel würden wir normalerweise verschiedene Prognosemodelle für verschiedene Zeitreihen ausprobieren. In diesem Artikel wollten wir den Schwerpunkt auf die verschiedenen Methoden der Imputation und deren Bewertung legen.

Fazit & Tipps zur Anwendung

Zusammenfassend lässt sich sagen, dass man immer mit einer Analyse der Zeitreihendaten beginnen und untersuchen sollte, ob die Daten zufällig fehlen oder ob es bestimmte Muster gibt. Im letzteren Fall sollte man versuchen, mit Hilfe eigenen Fachwissens oder durch Konsultation von Experten auf dem Gebiet Erklärungen zu finden. So sollte man sich beispielsweise bereits bei der Datenanalyse fragen, ob Lücken in regelmäßigen Abständen auftreten, wie lang die Lücken sind und wie hoch der prozentuale Anteil der fehlenden Daten im Verhältnis zur Gesamtgröße ist. Die Beantwortung dieser Fragen wird schon oft Aufschluss geben und dabei helfen, entweder spezifische Lösungen oder geeignete Imputationsmethoden nach unserer Faustregel zu finden.

Auch wenn die vorgestellte Regel ein guter Anhalts- und Ausgangspunkt für die Wahl der geeigneten Imputationsmethode ist, so ist es auch notwendig, diese immer mit Bedacht zu bewerten. Dabei ist es enorm wichtig und hilfreich, eine visuelle Bewertung mit einer analytischen zu kombinieren – wie bei jedem Prognosemodell.   

Man sollte bei der visuellen Auswertung darauf achten, welche Methode am besten zum Muster der Zeitreihe passt. Für die analytische Auswertung können die imputierten Werte aus verschiedenen Imputationsmethoden verwendet werden, um Prognosemodelle zu trainieren und diese auf einem Testsatz der Daten zu bewerten.  Dieser Ansatz ist sinnvoll, weil das Ziel der Imputation darin besteht, gute Vorhersageergebnisse zu erzielen. Gängige Forecasting-Metriken wie MAE oder SMAPE können für die Auswertung nützlich sein – aber die geeignete Metrik hängt immer von den spezifischen Geschäftszielen ab.