Mit diesem Beitrag wollen wir die Brücke schlagen zwischen dem grundlegenden Verständnis von Reinforcement Learning (RL) und dem Lösen eines Problems mit RL-Methoden. Der Artikel ist in drei Abschnitte unterteilt. Der erste Abschnitt ist eine kurze Einführung in RL. Der zweite Abschnitt erklärt die wichtigsten Begriffe, die zur Formulierung eines RL-Problems erforderlich sind, anhand eines Beispiels. Im dritten und letzten Abschnitt stellen wir schließlich eine grundlegende Implementierung zur Lösung eines Problems mit RL vor.

Was ist Reinforcement Learning?

Reinforcement Learning (RL) ist eine Art des Maschinellen Lernens. Es geht dabei darum, Agenten zu trainieren, Entscheidungen in einer Umgebung zu treffen, indem sie aus den Folgen ihrer Handlungen lernen. Der Agent erhält Rückmeldungen in Form von „Belohnungen“ oder „Bestrafungen“, die er nutzt, um seine Entscheidungsstrategie zu aktualisieren und seine Leistung mit der Zeit zu verbessern. Der Agent lernt durch Trial-and-Error, d. h. er probiert verschiedene Aktionen aus und erhält Rückmeldungen in Form von Belohnungen oder Bestrafungen. RL kann für jeden Prozess oder jedes System verwendet werden, das einen sequenziellen Entscheidungsfindungsprozess beinhaltet, der optimiert werden könnte.

RL findet Anwendung in Bereichen wie autonomes Fahren, Robotik, Kontrollsysteme, Spiele-KI sowie Wirtschaft und Finanzen, z. B. bei der Optimierung der Entscheidungsfindung in der Portfolio-Optimierung und der Ressourcenzuweisung. Außerdem wurde es zur Verbesserung der Leistung von Dialogsystemen (Chatbots) wie ChatGPT eingesetzt, die in den letzten Monaten für viel Wirbel gesorgt haben.

Reinforcement Learning – Beispiel & Definitionen

Dieser Abschnitt gibt einen Überblick über die Definitionen und Beschreibungen der wichtigsten Begriffe, die zum Verständnis der Dynamik von RL-Algorithmen erforderlich sind. Es ist immer einfacher, komplexe Begriffe anhand eines einfachen visuellen Reinforcement-Learning-Beispiels zu verstehen, daher wollen die verschiedenen Begriffe im Folgenden mithilfe eines einfachen Problems des Reinforcement Learning erklären.

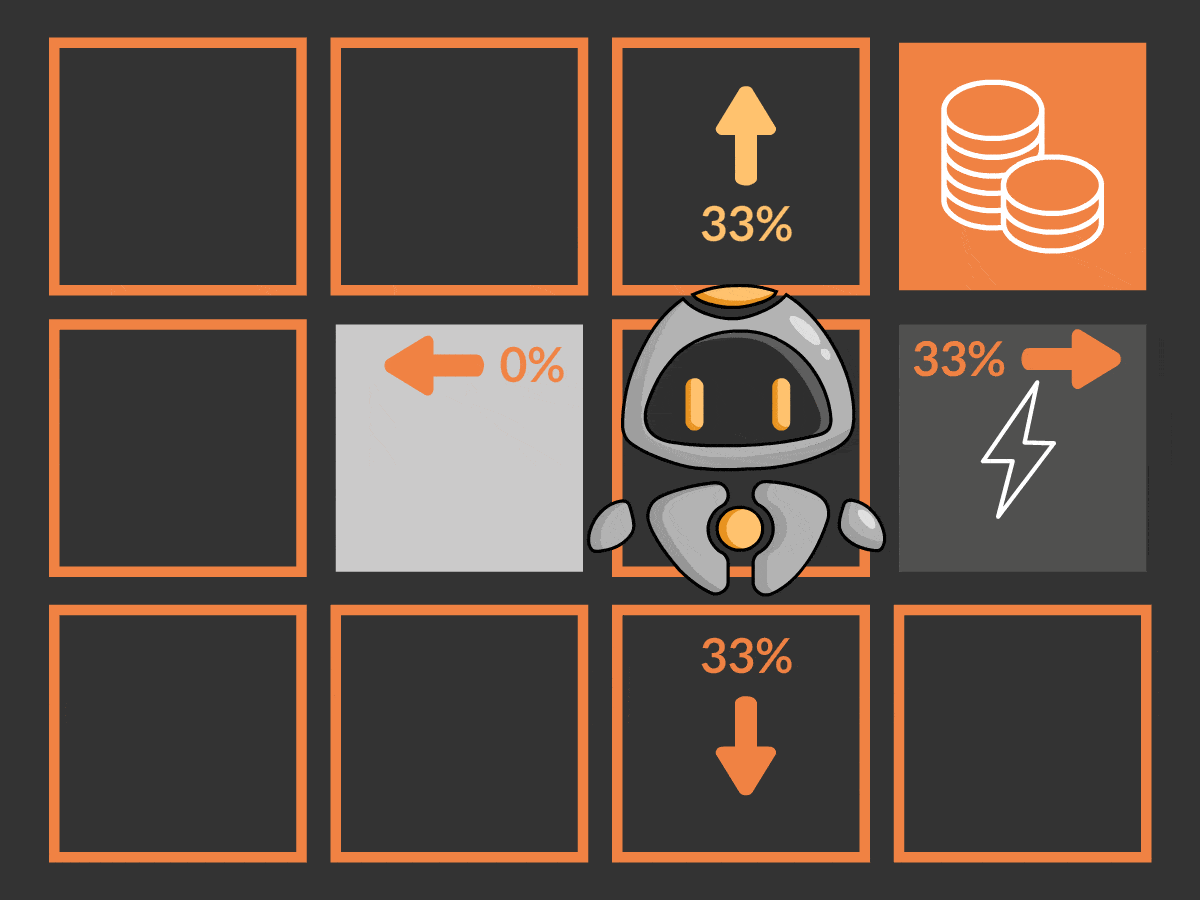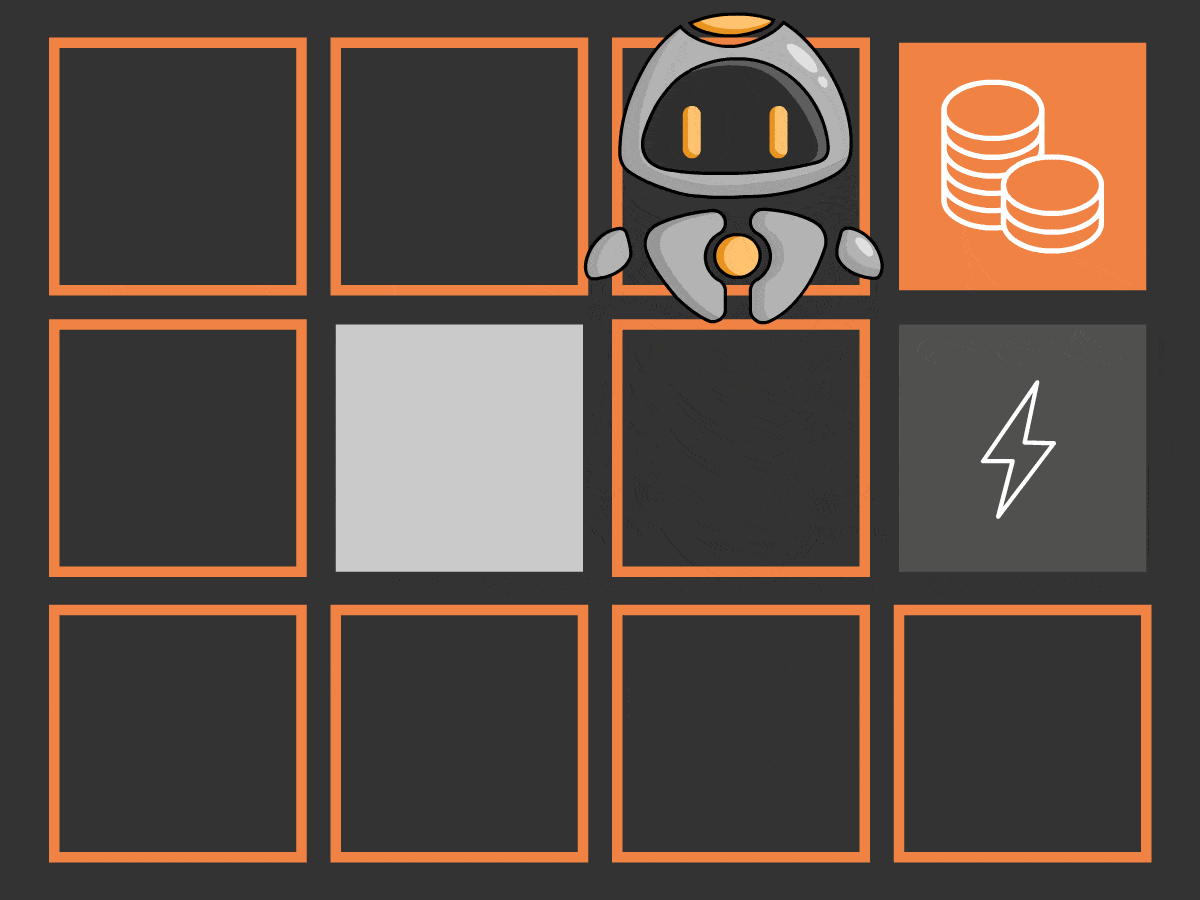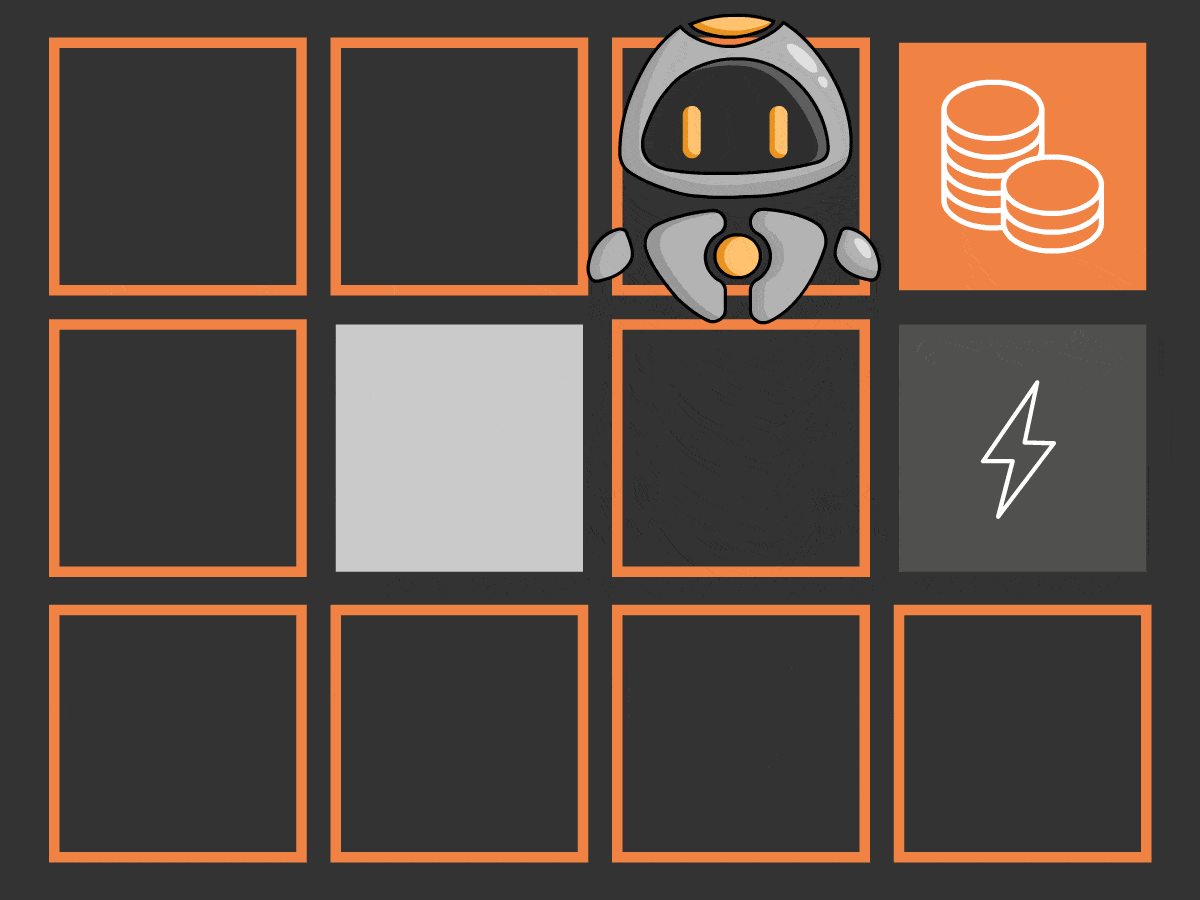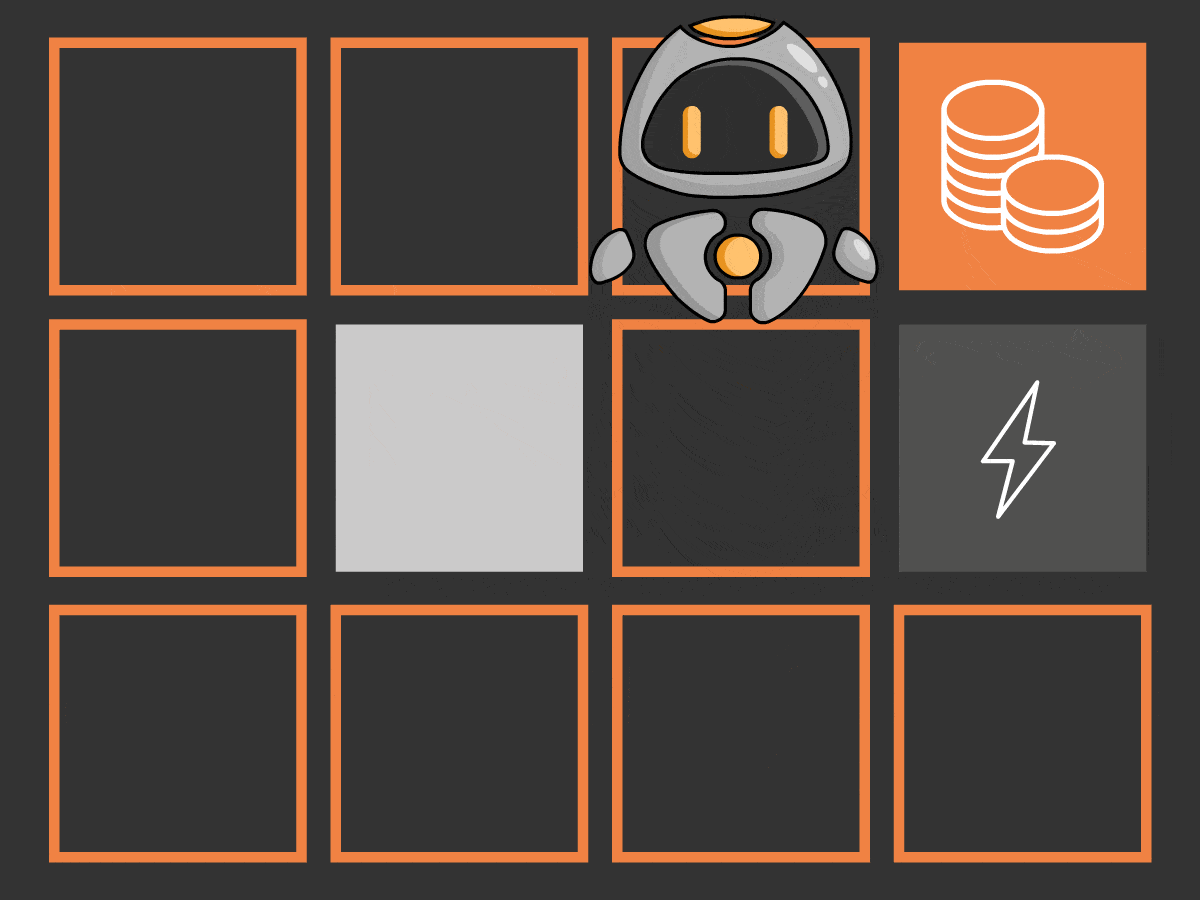
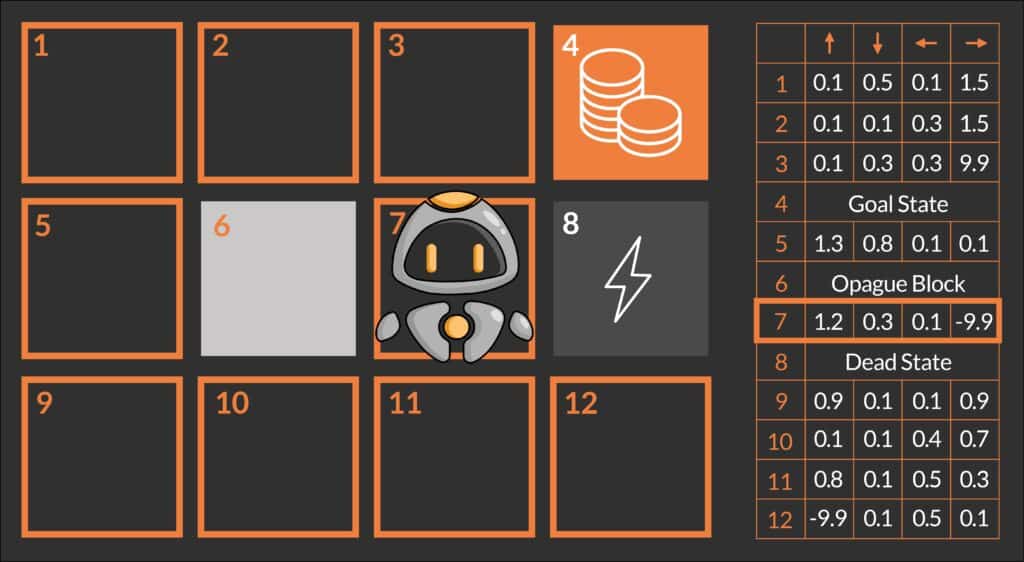
Das Hauptziel unseres Roboters QT ist es, das Spiel zu gewinnen, indem er das Zielfeld (auch als Zielzustand bekannt), das durch Münzen gekennzeichnet ist, erreicht, indem er den optimalen Weg findet und verfolgt. Um sich im Labyrinth zu bewegen, kann QT vier Aktionen ausführen: nach oben, nach unten, nach links und nach rechts gehen. In dieser Umgebung gibt es einige Hindernisse wie das Blitz-Feld und den unpassierbaren Block (grauer Kasten). Diese Hindernisse können QT entweder töten oder ihn daran hindern, seine beabsichtigte Aktion (Bewegung) auszuführen. Da QT keine Vorkenntnisse über das Labyrinth hat, besteht die Idee darin, dass QT versucht, die Umgebung durch zufälliges Navigieren zu erkunden und einen möglichen Weg zum Ziel zu finden.

Um besser zu verstehen, wie QT dies erreichen kann, ist es wichtig, einige grundlegende RL-Komponenten und Begriffe zu verstehen, die auch verwendet werden, um das Problem mathematisch zu formulieren.

Das Labyrinth wird als Umgebung (Environment) und der Roboter QT als Agent bezeichnet. Beim Reinforcement Learning ist die Umgebung das System, die Simulation oder der Raum, in dem der Agent agieren kann. Das Wichtigste ist, dass der Agent die Regeln oder die Dynamik der Umgebung in keiner Weise verändern kann. Die Umgebung ist die Welt des Agenten, in der er interagiert, indem er bestimmte Aktionen ausführt und Rückmeldungen erhält. Der Agent interagiert mit der Umwelt und trifft Entscheidungen. Dabei kann es sich um einen Roboter, ein Softwareprogramm oder ein anderes System handeln, das Aktionen ausführen und anschließend eine Belohnung erhalten kann. Im obigen Beispiel interagiert QT (der RL-Agent) mit dem Labyrinth (Umgebung), indem er sich in eine der Richtungen bewegt und seine Position im Labyrinth aktualisiert. Nachfolgend die verschiedenen Komponenten und Merkmale der Agenten-Umwelt-Interaktion:

Eine kompakte Einleitung in die Definition und Begrifflichkeiten hinter Reinforcement Learning erhalten Sie in unserem Grundlagenartikel zur Methodik:

Reinforcement Learning: kompakt erklärt

Reinforcement Learning Fundamental-Definitionen

1. State (Zustand): Die Parameter oder Beobachtungen, die die Umgebung des Agenten beschreiben, werden zusammenfassend als Zustand der Umgebung (=state) bezeichnet. Er umfasst alles, was der Agent über die Umgebung beobachten kann, sowie alle internen Variablen des Agenten, die für die Aktionen des Agenten relevant sein können. Im obigen Reinforcement-Learning-Beispiel ist der Zustand des Roboters seine Position im Labyrinth. Einige Umgebungen, wie das obige Beispiel, haben spezielle Zustände, die terminale Zustände genannt werden und den Zielzustand (Münzen-Feld) und andere Endzustände (Blitz-Feld) enthalten. Ein terminaler Zustand ist der Zustand der Umgebung, bei dessen Erreichen der Agent nicht in der Lage ist, weiterzugehen. In diesem Fall beendet der Agent seinen aktuellen Lernzyklus und es beginnt ein neuer Lernzyklus mit dem neu gewonnenen Wissen über die Umwelt.
   
   
2. Action: Eine Aktion ist eine vom Agenten getroffene Entscheidung und stellt das Mittel der Interaktion des Agenten mit der Umwelt dar. Es kann sich dabei um eine physische Bewegung, eine Änderung des internen Zustands des Agenten oder jede andere Art von Entscheidung handeln, die der Agent treffen kann. Die Folgen der vom Agenten durchgeführten Aktionen sind die Veränderung des Umweltzustands und die Rückmeldungen, die er erhält. Im obigen Reinforcement-Learning-Beispiel hat unser Roboter vier mögliche Aktionen (nach oben, nach unten, nach links oder nach rechts), die er ausführen kann, um seinen Zustand zu ändern.
   
   
3. Reward (Belohnung):  Wenn ein Agent eine Aktion durchführt, gibt die Umgebung nicht nur eine Rückmeldung in Form des neuen Zustands, sondern auch ein Belohnungssignal. Eine Belohnung stellt den Nutzen dar, den der Agent beim Eintritt in den neuen Zustand auf der Grundlage seiner zuletzt durchgeführten Aktion hat. Die Belohnungskomponente ist im RL von größter Bedeutung, da sie den Agenten bei der Suche nach dem optimalen Pfad oder Prozess leitet. Die Konzepte im nächsten Abschnitt erklären, dass der Agent im Wesentlichen versucht, die kumulative Belohnung zu maximieren, die er von der Umgebung erhält, um den kürzesten Weg zu finden, wie es im obigen Beispiel für QT der Fall ist. In dem Beispiel beträgt die Belohnung für den Agenten, der auf den Zielzustand (Münzen) tritt, +10 Punkte, die Belohnung für den Agenten, der auf das Blitz-Feld tritt, ist -10 Punkte und für alle anderen Zustände könnte sie 0 oder -1 Punkt betragen.
   
   
4. Transition Probability (Übergangswahrscheinlichkeit): Sie ist eine der wichtigsten Eigenschaften für einige der Umgebungen. Sie definiert die Wahrscheinlichkeit, von einem Zustand in einen anderen zu gelangen, indem eine bestimmte Aktion im aktuellen Zustand ausgeführt wird. Dieser Parameter legt fest, ob die Umgebung stochastisch oder deterministisch ist. Dementsprechend kann das Verhalten des Agenten in der gleichen Umgebung unterschiedlich sein. Anhand eines Beispiels lässt sich dieses Konzept leichter verstehen.
   
   • Deterministische Umgebung: Für solche Umgebungen wird die Übergangswahrscheinlichkeit auf 1 gesetzt. Das bedeutet, dass der Übergang des Agenten von einem Zustand in einen anderen nur durch die Aktion bestimmt wird, die er im aktuellen Zustand ausführt. Wenn QT im folgenden Beispiel beschließt, sich nach rechts zu bewegen, würde er im Blitz-Feld landen und definitiv sterben! Entscheidet es sich dagegen für eine Bewegung nach oben, wäre es dem Zielzustand einen Schritt näher. Für den Rest des Artikels wird die Umgebung deterministisch bleiben.

• • Stochastische Umgebung: In solchen Umgebungen wird der Übergang des Agenten von einem Zustand in einen anderen durch die Aktion, die er ausführt, sowie durch die Verteilung der Übergangswahrscheinlichkeit bestimmt, die festlegt, in welche Zustände er übergehen kann. Die Übergangswahrscheinlichkeiten können wie folgt definiert werden (aus dem Frozen lake Problem): Der Agent bewegt sich mit einer Wahrscheinlichkeit von 1/3 (33%) in die von ihm beabsichtigte Richtung oder mit der gleichen Wahrscheinlichkeit von 1/3 (33%) in eine senkrechte Richtung, wie unten dargestellt. Angenommen, QT beschließt, sich nach rechts zu bewegen, dann ist die Wahrscheinlichkeit, dass er im Blitz-Feld landet, 33 % und in einem der beiden Blöcke oben und unten mit je 33 % zu landen. Das bedeutet, dass QT im Gegensatz zu der obigen Umgebung, in der es um jeden Preis vermeiden muss, sich nach rechts zu bewegen, um zu überleben, jetzt eine Aktion durchführen kann, um sich nach rechts zu bewegen, da dies eine Überlebenschance von 66 % bietet.

5. Exploration vs. Exploitation (Erkundung vs. Ausbeutung): In RL sind Exploration und Exploitation zwei Konzepte, die sich auf das Gleichgewicht zwischen dem Ausprobieren neuer Aktionen zur Erkundung neuer Zustände (Exploration) und dem Ergreifen der besten bekannten Aktion im aktuellen Zustand (laut QTs derzeitiger Einsätzung) zur Erzielung der größtmöglichen Belohnung (Exploitation) beziehen.
   
   
   • Während der Erkundungsphase probiert der Agent neue Aktionen aus, um mehr über die Umgebung zu erfahren und seine Entscheidungsfindung zu verbessern. Dies hilft dem Agenten, Zustände mit hoher Belohnung zu entdecken und Aktionen durchzuführen, um diese zu erreichen. In der Ausbeutungsphase versucht er, die Endzustände auf die optimale Weise zu erreichen, um die kumulative Belohnung zu maximieren. Im obigen Reinforcement-Learning-Beispiel würde QT zunächst Aktionen ausprobieren, um verschiedene Zustände und mögliche Wege zum Ziel zu entdecken. Manchmal wird es im Blitz-Feld und manchmal im Münzen-Feld enden, aber es wird Wissen sammeln und lernen, welche Zustands-Aktions-Kombinationen zu diesen Zuständen führen. Mit zunehmender Erfahrung wird es allmählich lernen, den optimalen Weg (in unserem Beispiel den kürzesten Weg) zu finden.
     
     
   • Das Gleichgewicht zwischen Erkundung und Ausbeutung wird oft als exploration-exploitation trade-off bezeichnet. Im Allgemeinen gilt: Je mehr ein Agent erforscht, desto mehr Wissen gewinnt er über die Umwelt, aber es kann länger dauern, bis er die höchste Belohnung erhält und die optimale Strategie findet. Andererseits kann ein Agent, je mehr er ausbeutet, desto schneller eine höhere Belohnung erzielen, aber er findet nicht unbedingt die optimale Strategie und verpasst die Entdeckung von sehr lohnenden Zuständen. Im Folgenden werden einige gängige Strategien beschrieben, die dazu beitragen, ein Gleichgewicht zwischen Erkundung und Ausbeutung herzustellen:
     
     
     • Epsilon-Greedy-Algorithmus (ε-greedy) Bei diesem Algorithmus beginnt der Agent mit einer hohen Erkundungswahrscheinlichkeit (ε) und einer niedrigen Ausnutzungswahrscheinlichkeit (1-ε). Dies ermöglicht es dem Agenten, anfangs neue Aktionen zu erforschen und nach und nach die besten bekannten Aktionen aus der Erfahrung zu nutzen. Die Änderungsrate des Wertes von ε ist ein Hyperparameter, der von der Komplexität des RL-Problems abhängt. Sie kann linear, exponentiell oder durch einen mathematischen Ausdruck definiert sein.
       
       
     • Obere Konfidenzgrenze (Upper Confidence Bound = UCB): Bei diesem Algorithmus wählt der Agent eine Aktion auf der Grundlage des Gleichgewichts zwischen der erwarteten Belohnung und der Unsicherheit der Aktion. Dies ermöglicht es dem Agenten, Aktionen mit hoher Unsicherheit zu erkunden, aber auch Aktionen mit hohen erwarteten Belohnungen zu nutzen. In UCB behält der Agent eine Schätzung der erwarteten Belohnung jeder Aktion sowie ein Maß für die Unsicherheit der Schätzung. Der Agent wählt die Aktion mit dem höchsten „Upper Confidence Bound“-Wert), der sich aus der Summe der erwarteten Belohnung und einem Term ergibt, der die Unsicherheit der Schätzung darstellt. Der Unsicherheitsterm wird häufig als Quadratwurzel des natürlichen Logarithmus der Gesamtzahl der gewählten Aktionen gewählt. Die Intuition dahinter ist, dass die Unsicherheit der Schätzung mit zunehmender Anzahl der gewählten Aktionen abnehmen sollte, da der Agent mehr Daten hat, auf die er seine Schätzung stützen kann.

Mathematische Formulierung der Terminologien anhand des Reinforcement-Learning-Beispiels

Nachdem wir die grundlegende Terminologie im Zusammenhang mit dem „Labyrinth-Problem“ kennengelernt haben, wollen wir diese Terminologie aus einer mathematischen Perspektive formulieren und verstehen.

1. Der Roboter QT (Agent) erhält den Zustand S₀ von der Umgebung – den aktuellen Block des Roboters in der Umgebung
2. Basierend auf diesem Zustand S₀ führt QT (Agent) eine Aktion A₀ aus – sagen wir, QT bewegt sich nach oben
3. Die Umgebung wechselt in einen neuen Zustand S₁ – neuer Block
4. Die Umgebung gibt dem Agenten eine Belohnung R₁ – QT ist noch nicht tot (positive Belohnung, +1)
5. Die Übergangswahrscheinlichkeit wird als P(S₁ | S₀, A₀) oder T bezeichnet – hier ist sie 1, da die Umgebung von Natur aus deterministisch ist

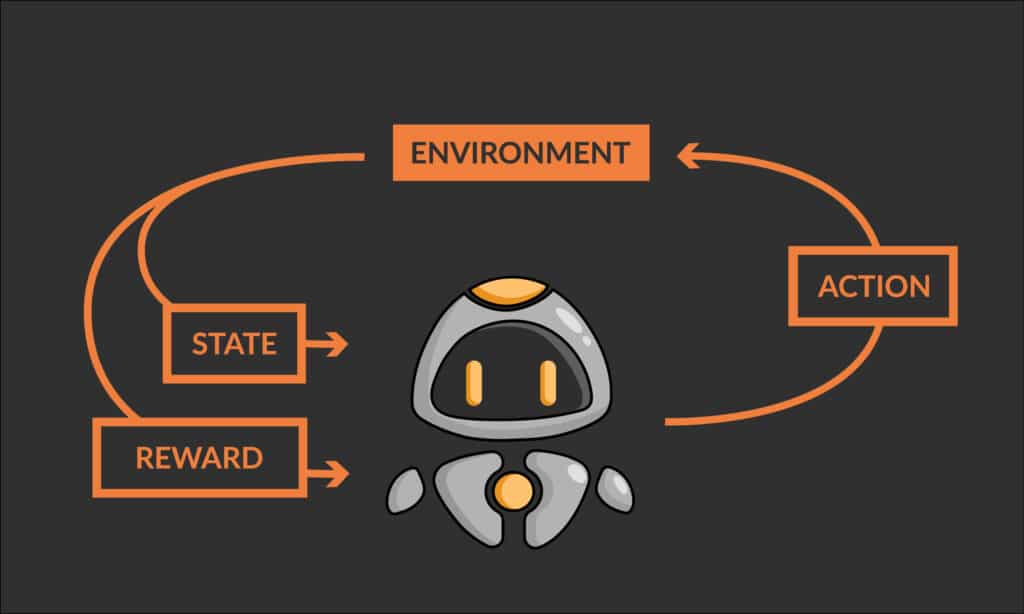
Die obige Schleife stellt einen Schritt des Agenten dar. Der Agent muss mehrere solcher Schritte {S₀, A₀, R₁, S₁, T₀} unternehmen, um seine Umgebung zu erkunden und die guten und schlechten Zustände zusammen mit den jeweiligen Aktionen, die zu ihnen führen, zu identifizieren. Und schließlich muss er auf dem optimalen Weg zum Ziel navigieren. Um nun ein Entscheidungs- oder Optimierungsproblem mit Hilfe von Reinforcement Learning zu formulieren und zu lösen, müssen einige sehr wichtige Konzepte und Begriffe erklärt werden.

In unserem Deep Dive beleuchten wir die Wechselwirkungen zwischen Geschäftsmethoden, Neurowissenschaften und dem Reinforcement Learning in künstlicher und biologischer Intelligenz.

Reinforcement Learning – Algorithmen im Gehirn

DISCLAIMER: Jetzt beginnt ein mathematischer Deep Dive!

Mathematische Modellierung eines Entscheidungsproblems

1. Markov Decision Process = MDP: Ein Markov-Entscheidungsprozess ist ein Prozess, bei dem die zukünftigen Zustände nur vom gegenwärtigen Zustand abhängen und in keiner Weise mit den vergangenen Zuständen verbunden sind, die zum gegenwärtigen Zustand geführt haben. Dieser mathematische Rahmen wird zur Modellierung von Entscheidungsproblemen beim Reinforcement Learning verwendet. Bei einer Abfolge von Zuständen, Aktionen und den Belohnungen s0, a0, r0, s1, a1, r1, s2, a2, r2….st, at, rt (die so genannte Historie), die von einem Agenten beobachtet wird, wird gesagt, dass das Zustandssignal die Markov-Eigenschaft hat, wenn es die folgende Gleichung erfüllt:
P (S_t+1 = s′, R_t+1 = r′| s_t, a_t) = P (S_t+1 = s′, R_t+1 = r′| s_t, a_t, r_t, … s₀, a_0, r₀), wo:

• S ist eine Menge von Zuständen, S = {s0, s1, …}
• A ist eine Menge von Aktionen, A = {a0, a1, …}
• T ist eine Menge von Übergangswahrscheinlichkeiten, T = {P(st+1|st, At), P(st+2|st+1, At+1), P(st+3|st+2, At+2), …}
• R ist eine Menge von Belohnungen, R = {r0, r1, …}

2. Cumulative Return and Discount Factor (Kumulierte Rendite und Abzinsungsfaktor)

a) RL-Agenten lernen, indem sie eine Aktion auswählen, die die kumulative zukünftige Belohnung maximiert. Die kumulative zukünftige Belohnung wird Rendite (return) genannt und oft mit R bezeichnet. Die Rendite zum Zeitpunkt t wird wie folgt bezeichnet:

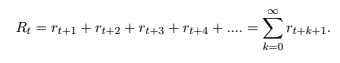
b)  Diese Gleichung ist nur sinnvoll, wenn die Lernaufgabe nach einer kleinen Anzahl von Schritten endet. Wenn die Lernaufgabe viele sequenzielle Entscheidungen erfordert (z. B. das Ausbalancieren einer Stange), ist die Anzahl der Schritte hoch (oder sogar unendlich), so dass der Wert der Rendite unbegrenzt sein kann. Daher ist es gebräuchlicher, die zukünftige kumulative diskontierte Belohnung G (cumulative discounted reward G) zu verwenden, die wie folgt ausgedrückt wird:

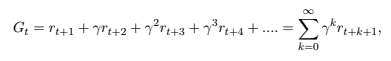
Wobei γ als Diskontierungsfaktor bezeichnet wird und im Bereich von [0, 1] variiert. Gamma (γ) steuert die Bedeutung der zukünftigen Belohnungen gegenüber den unmittelbaren Belohnungen. Je niedriger der Abzinsungsfaktor (näher an 0) ist, desto weniger wichtig sind die zukünftigen Belohnungen, und der Agent wird dazu neigen, sich nur auf die Handlungen zu konzentrieren, die maximale unmittelbare Belohnungen bringen. Wenn der Wert von γ höher ist (näher an 1), bedeutet dies, dass jede zukünftige Belohnung gleich wichtig ist. Wenn der Wert von γ auf 1 gesetzt wird, dann ist der Ausdruck für die kumulative Diskontbelohnung G derselbe wie der für die Rendite R.

3. Policy: Eine Policy (bezeichnet als π(s)) ist ein Satz von Regeln oder ein Algorithmus, den der Agent verwendet, um seine Aktionen zu bestimmen. Diese Policy legt fest, wie sich der Agent in jedem Zustand verhält und welche Aktion er in einem bestimmten Zustand wählen soll. Für einen Agenten ist eine Policy eine Abbildung von Zuständen auf ihre jeweiligen optimalen Aktionen. Zu Beginn, wenn der Agent mit dem Lernen beginnt, besteht eine Policy aus einer Zuordnung von Zuständen zu zufälligen Aktionen. Während des Trainings erhält der Agent jedoch verschiedene Belohnungen aus der Umgebung, die ihm helfen, die Policy zu optimieren. Die optimale Policy ist diejenige, die es dem Agenten ermöglicht, den Ertrag in jedem Zustand zu maximieren. Die optimale Policy wird mit π* bezeichnet und ist eine Abbildung von Zuständen auf die jeweiligen optimalen Aktionen in diesen Zuständen.

4. Action Value and State Value Functions (Aktionswert- und Zustandswertfunktionen): Um die Policy zu optimieren, muss der Agent zwei Dinge herausfinden. Erstens, welches die guten und schlechten Zustände sind, und zweitens, welche Aktionen für jeden Zustand die guten und schlechten sind. Zu diesem Zweck können zwei verschiedene Wertfunktionen verwendet werden, nämlich die Zustandswertfunktion V(s) und die Aktionswertfunktion Q(s,a).

a) State value function – Die Zustandswertfunktion definiertdefiniert die „Güte“ des Agenten, der sich in einem Zustand befindet.. Mathematisch gesehen schätzt die Zustandswertfunktion den erwarteten zukünftigen Nutzen eines bestimmten Zustands. Diese Werte geben den erwarteten Ertrag an, wenn man von einem Zustand ausgeht und seine Policy π verfolgt.

Sie wird als V(s) oder Vπ(s) bezeichnet, wobei s der aktuelle Zustand ist. Er ist mathematisch definiert als:

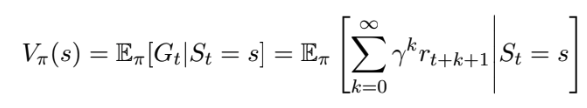
b) Action value function Die Handlungswertfunktion bewertet „die Qualität einer Handlung in einem Zustand“, d.h. wie gut eine bestimmte Handlung in einem bestimmten Zustand ist. Mathematisch gesehen schätzt sie den erwarteten zukünftigen Nutzen einer bestimmten Handlung in einem bestimmten Zustand und der anschließenden (erneuten) Befolgung der Strategie. Sie ist ähnlich wie die Zustandswertfunktion, nur dass sie spezifischer ist, da sie die Qualität jeder Handlung in einem Zustand und nicht nur den Zustand selbst bewertet.

Sie wird als Q(s,a) oder Qπ(s,a) bezeichnet, wobei s der aktuelle Zustand und a die durchgeführte Aktion ist:

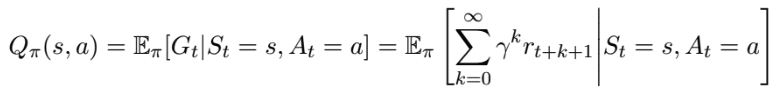
5. Bellman Equation (Bellman-Gleichung): Die Bellman-Gleichung ist grundlegend für die Schätzung der beiden Wertfunktionen. Sie definiert die Beziehung zwischen dem aktuellen Zustands-Aktionspaar (s, a), der beobachteten Belohnung und den möglichen Nachfolge-Zustands-Aktionspaaren. Diese Beziehung wird verwendet, um die optimale Wertfunktion zu finden. Die Bellman-Gleichung definiert den Wert eines Zustands-Aktionspaares Q(s,a) als die erwartete Belohnung für die beste Aktion in diesem Zustand s plus den diskontierten Wert des besten nächsten Zustands-Aktionspaares (gemäß der aktuellen Policy).

Die Bellman-Funktion kann sowohl für die Zustands-Wert-Funktion V(s) als auch für die Handlungs-Wert-Funktion Q(s, a) wie folgt definiert werden:

V(s) = max(a) [R(s,a) + γ * V(s‘)]

Q(s,a) = R(s,a) +  γ * max(a‘) [Q(s‘,a‘)], wo

• V(s) der Wert des Zustands s ist
• Q(s,a) die Aktionswertfunktion für die Durchführung der Aktion a im Zustand s ist
• s‘ der nächste Zustand ist
• a‘ die nächste Handlung ist
• γ der Diskontierungsfaktor Gamma ist
• max(a) der maximale Wert über alle möglichen Aktionen ist

Vertiefen Sie Ihr Verständnis für das Konzept der „Tödlichen Triade“ im Reinforcement Learning, seine Auswirkungen und Lösungsansätze. Dieser Deep Dive versorgt Sie mit einem Überblick über RL-Konzepte, Vorstellung der „Tödlichen Triade“ und deren Bewältigungsstrategien.

Reinforcement Learning – Deadly Triad

Die Implementierung von Reinforcement Learning

Das Verfahren zur schrittweisen Schätzung der Aktionswerte aus den beobachteten Zustands-Aktions-Belohnungs-Zustands-Tupeln wird als Q-Learning bezeichnet. Die Q-Werte werden anhand der Bellman-Gleichung aktualisiert:

1. Q(s, a) = Q(s, a) + α * (R(s,a) + γ * max(a‘) [Q(s‘, a‘)] – Q(s, a)), wobei

• Q(s,a) der Q-Wert für die Durchführung von Aktion a im Zustand s ist
• R(s,a) die unmittelbare Belohnung für die Ausführung von Aktion a im Zustand s ist
• s‘ der nächste Zustand ist
• a‘ die nächste Handlung ist
• γ der Diskontierungsfaktor gamma ist
• α die Lernrate alpha ist

2. Q-Tables: Q-Tabellen sind eine Datenstruktur (zweidimensionale Tabelle), in der alle möglichen Aktionswerte Q(s,a) gespeichert werden. Jeder Eintrag in der Tabelle stellt den Q-Wert für ein bestimmtes Zustands-Aktionspaar dar. Die Q-Tabelle ist anfangs mit beliebigen Werten (oder Nullen) gefüllt und wird im Laufe der Zeit aktualisiert, wenn der Agent neue Zustände entdeckt und beim Übergang in diese Zustände Belohnungen erhält. Aus der Q-Tabelle wird die Policy abgeleitet, um die beste Aktion für jeden Zustand zu bestimmen. In dem obigen Beispiel gibt es 12 Zustände (3 x 4 Raster) und 4 Aktionen (auf, ab, links, rechts). Daher ist die Q-Tabelle eine Matrix mit 12 Zeilen (eine für jeden Zustand) und 4 Spalten (eine für jede Aktion).
   
   
3. Für das Training des Reinforcement Learning Agenten (Training bedeutet Schätzung von Q-Werten) ist eine iterative Interaktion des Agenten mit der Umwelt erforderlich. Dieses Training wird in Episoden durchgeführt: Eine Episode bezieht sich auf einen einzelnen Durchlauf der Agenten-Umwelt-Interaktion, der mit einem Anfangszustand (oder Startzustand) beginnt und an einem Endzustand endet oder wenn eine bestimmte Anzahl von Schritten durchgeführt wurde. Eine Episode besteht aus allen Entscheidungen, die ein Agent während dieser einzelnen Interaktion trifft. Im obigen Beispiel endet die Episode, wenn QT einen der Endzustände – Blitz- oder Münzen-Feld – erreicht. Dies liegt daran, dass QT im Blitz-Feld getötet wird und das Training neu gestartet werden muss. Im Münzen-Feld hat QT sein Ziel erfolgreich erreicht und das Training muss neu gestartet werden, um seine Leistung zu verbessern. Sobald QT trainiert und die Q-Tabelle optimiert wurde, kann die optimale Strategie (oder „optimale Policy“) durch Auswahl der besten Aktion (höchster Wert der erwarteten zukünftigen Belohnung) für jeden Zustand extrahiert werden. Die Q-Tabelle könnte etwa so aussehen:

Über den Einsatz von Reinforcement Learning in der Industrie und anderen relevanten Branchen lesen Sie in unserem Fachbeitrag:

Reinforcement Learning – Use Cases für Unternehmen